|
|
|
OPTIMAL
SPHERICAL PACKING OF CIRCLES
AND
HILBERT'S 14TH PROBLEM
JAMES R. VAN DYKE
jvandyke@slip.net
Abstract:
We discover a system of mathematics that provides positive examples for
the 14th problem of Hilbert, two new families of polytopes, a master Abelian
rotational group Gf'PnXGfPnfor
the polytopes, twelve unique solution sets for the optimal spherical packing
of circles, and the foundations for a sexagesimal analytic geometry. Over
the surface of a hyper-complex sphere, the optimal spherical packing of
circles are defined by a regular system of points that are an integer number
of degrees from their closest neighbors and their coordinates, (Z2,...,Z2),
provide integer solutions sets for polynomial equations with integer coefficients.
Using unitary diagonal matrices as elements (labels), the closed geometrically
finite groups of the Tetrahedral, the Octahedral, and the Icosahedral
(and their dual groups) are combined into the master Abelian rotational
group, Gf'P3XGfP3,
when n = 3. The group geometry defines the polytopes over
a spherical projection plane with the matrix algebra and demonstrates that
the 14th problem of Hilbert has positive examples over a hyper-complex
sphere. The extension fields take into consideration chirality and
invariance over a unified commuting vector field. The
orthogonal rotational group Z2,Z2,Z2,Z2,Z2,Z2
is isomorphic to the symmetric group S6, which
is solvable when defined by Gf'P3XGfP3
and labeled with matrices. The group is then extended to include
semi-regular polytopes when n = 6, 12.
OPTIMAL SPHERICAL
PACKING OF CIRCLES AND HILBERT'S 14TH PROBLEM
INTRODUCTION.1
A geometry of circles, geodesics, and spheres has existed for the last
five millennia. Unfortunately, the knowledge that the ancient Sumerians
used to define their analytic geometry was lost during the millennium preceding
the great mathematical achievements of the Greek civilization. The
following research did not start with the search for a Sumerian analytic
geometry, but instead, for a mathematical method to deal with the fact
that there exists two systems of coordinates (left-handed and right-handed).
The solution to their unification is very fruitful and is the portal to
the discovery of many interesting aspects of mathematics that includes
the foundation for a Sino-Sumerian analytic geometry based on spherical
polytopes. The investigation into the invariant nature of objects
possessing a sense or handedness leads to discoveries about the structure
of curved space and it leads to Hilbert's 14th problem. Hilbert
asks, does an example exist for the finiteness of certain systems of relative
integral functions? He then stipulates that the solutions and the coefficients
of the polynomial equations are to be integers.
We
use a geometric approach to the 14th problem, where positive finite extension
fields are developed over a unit sphere by modeling larger and larger polytopes.
The 14th problem of Hilbert has not yet been completely solved, however,
a geometric program has been found that will lead to its solution and the
reconstruction of the Sino-Sumerian sexagesimal analytical geometry.
In the following examples, algebra, geometry, group theory, linear algebra,
and number theory are woven together to demonstrate positive geometric
examples to Hilbert's 14th problem based on spherical polytopes.
In the process of dividing the surface of the sphere into smaller and smaller
congruent parts, we discover a master Abelian rotational group Gf'PnXGfPnfor
the polytopes, two new families of polytopes, twelve unique solution sets
for the optimal spherical packing of circles, and the foundation for a
sexagesimal analytic geometry.
At
the International Congress in Paris in 1900, Hilbert [4a]
delivered the opening lecture and offered samples of 23 problems to be
solved during the new century. The 14th problem remained unsolved
until 1959, when Nagata [5] presented counter
examples to the problem over the projection plane. A tetrahedron provides
a closed finite geometric system, in which a positive example is shown
to exists. The problem is solvable when the projection plane is the surface
of a sphere. A specialization of linear algebra and group theory combine
to form a closed finite geometric system. The rotational group for the
invariant midpoints of the tetrahedron’s edges is defined by Gf8.
The finite system is defined over an orthogonal vector field in dimension
three, which was left as a remaining open problem in Nagata’s paper.
Hilbert
then asks, if such a system exists, may the system be extended to a more
general case? We demonstrate that the answer is yes. The geometric system
of the tetrahedron is extendable to a more general case that includes all
the regular polytopes. The first extension considers the dual vector space
of proper and improper rotations, of the tetrahedron and its dual in
the mirror. The extension to Gf’8XGf8
and/or Gf64 creates ten tetrahedra [3b].
The invariant midpoints of the edges for all of the regular polytopes are
defined by these ten tetrahedra. The polytopes are contained as subgroups
in the group Gf64, of order Pn
and type (Z2,...,Z2), where
Z2
= ±1, P = 2 (which is prime), and the dimension
of n = 6. The Abelian rotational group Gf64
is
the master rotational group for the regular polytopes.
A
complete system of functions incorporates the concept of handedness in
the system. The invariant property of the group Gf64
describes handedness with five pair of chiral tetrahedra. They provide
the geometric foundation over a dual vector field for the algebraic proofs
of the existence and the finiteness of certain complete systems of functions.
Specifically, solution sets for algebraic systems of integral functions
exist when n = 3, 6, 12, which provide integer solutions
for the coefficients of polynomial equations of degree n that are
defined by known finite geometric sets of polytopes. The coordinates,
(Z2,...,Z2), define a regular
system of points that are the integer solutions sets for the polynomial
equations with integer coefficients. A polynomial over a field F in the
indeterminate value x is expressed by an equation, such that
f(x)
= c0xn + c1xn-1
+ ... + cn-1x + cn
= 0,
where
c0,
c1, c2,...,cn are elements
of F called coefficients of the polynomial. Integral functions,
as polynomials are sometimes referred to, are completely determined by
their coefficients. Polynomials are monic when the leading coefficient
is equal to one, c0 = 1. The solution sets are
restricted to the surface of a sphere when the last coefficient is equal
to one, cn = ±1.
[2]
The
foundation for a sexagesimal analytical geometry is based on group theory
that is defined by a regular system of points constructed from the orthogonal
structure of spherical polytopes. For every dual polytope pair,
the midpoints of their edges are coincident and their edges cross each
other in space at 90 degree angles (orthogonal). The problem of determining
the possible arrangements of the polytopes projected on the surface of
a sphere is purely geometrical. The objects define an arrangement of points
and such an arrangement is a regular system of points. A regular system
of points is defined by three properties:
DEFINITION
1.1. A regular system of points in space is to contain infinitely many
points, and the number of points of the system contained inside a sphere
is to go to infinity as the cube of the radius.
DEFINITION
1.2. Any finite region of a regular system of points is to contain
only a finite number of points.
DEFINITION
1.3. There exists a symmetry operation for each point of a regular
system of points, such that any point may be moved to coincide with any
other point, leaving the point field invariant.
The
first two defining properties are clear without any further explanation.
The third may be elaborated upon to insure the proper understanding. An
observer situated at some particular point of the system cannot determine,
by performing some measurements, at which point of the system he is positioned.
The reason for this phenomenon is the position of every point, relative
to any other point, is the same. To bring any point of the system into
coincidence with any other point of the system, there exists a motion through
space, such that every position occupied by a point of the system before
the motion is also occupied by a point of the system after the motion.
This type of motion leaves the point system unchanged, or what is known
as invariant. The movement is called a symmetry transformation and all
such movements form a transformation group. [4b]
DEFINITION
1.4. The optimal spherical packing of circles are defined by a regular
system of points that are an integer number of degrees from
their closest neighbors and the point's coordinates, (Z2,...,Z2),
provide integer solutions sets for polynomial equations with integer
coefficients.
Group
theory links the geometric ideas together with an isomorphism (a one to
one relationship) between sets of point fields for spherical analogs
of the polyhedron collectively termed polytopes, sets of point fields for
the optimal packing of circles, and solution sets for algebraic systems
of integral functions. The optimal spherical packing of circles for the
smallest group is the cuboctahedron. The representation fields for
the optimal packing of circles are old and new families of polytopes. The
algebra of the field is that of hyper-complex numbers of the form
(Z2,...,Z2),
where Z2 = ± 1, and they have an order
of Pn with P = 2. When n=
3, 6, 12, these hyper-complex numbers represent points on the surfaces
of a unitary hyper-complex sphere and the systems of extension fields,
Gf'PnXGfPn,
provides
positive examples for Hilbert's 14th problem.
Hilbert's 14th problem
is linked by the master group Gf'PnXGfPn
to the hyper-complex unitary solution fields of regular and semi-regular
spherical polytopes. The largest polytope, modulo 60, is a truncated
rhombic triacontahedron with 44,132 faces and 43,200 vertices (centers
of an optimal packing of circles that are one degree in diameter).
The polytope has three different types of regular spherical polygons for
faces, 12 pentagonal, 42,240 rhombic, and 1880 triangular, all of which
have edges of one degree. A little mathematics
12*5 +42,240*4+1880*3 = 60+168,960+5640 = 174,660/2 = 87,330 edges
shows that the polytope
obeys Euler's Formula for Polyhedra ,V - E + F
= 2, (43,200 -87,330 +44,132 = 2). The sets of the optimal spherical
packing of circles,
modulo 60, on the surface of a unit sphere are
12(60); 48(30);
108(20); 192(15); 300(12); 432(10);
1,200(6); 1,728(5);
2,700(4); 4,800(3); 10,800(2); and 43,200(1).
The
integers in parentheses are the diameters of the circles in degrees.
The twelve solution sets are positive geometric examples that satisfy Hilbert's
14th problem where the polynomial equations have integers for coefficients
and integers for solutions. Each solution set represents a polytope presented
in Table 1.5. First is the three polytope family of the truncated
rhombic triacontahedron and second is the ten polytope family of the
truncated
rhombic dodecahedron.
| POLYTOPE |
#EDGES |
#VERTICES |
#FACES |
#TRIANGLE |
#RHOMBIC |
#PENTAGON |
| 43,200
(1) |
87,330 |
43,200 |
44,132 |
1,880 |
42,240 |
12 |
| 10,800
(2) |
21,810 |
10,800 |
11,012 |
440 |
10,560 |
12 |
| 2,700
(4) |
5,430 |
2,700 |
2,732 |
80 |
2,640 |
12 |
| POLYTOPE |
#EDGES |
#VERTICES |
#FACES |
#TRIANGLE |
#RHOMBIC |
#SQUARE |
| 4,800
(3) |
13,932 |
4,800 |
9,134 |
8,672 |
|
462 |
| 1,728
(5) |
4,908 |
1,728 |
3,182 |
2,912 |
|
270 |
| 1,200
(6) |
3,372 |
1,200 |
2,174 |
1,952 |
|
222 |
| 432
(10) |
1,164 |
432 |
734 |
608 |
|
126 |
| 300
(12) |
792 |
300 |
494 |
392 |
|
102 |
| 192
(15) |
492 |
192 |
302 |
224 |
|
78 |
| 108
(20) |
264 |
108 |
158 |
104 |
|
54 |
| 48
(30) |
108 |
48 |
62 |
32 |
|
30 |
| 48
(30) |
96 |
48 |
50 |
8 |
12 |
30 |
| 12
(60) |
24 |
12 |
14 |
8 |
|
6 |
Table 1.5
The
twelve solution sets for the polytopes are generated by the optimal spherical
packing of circles, note that set 48(30) has two forms. Each of
the thirteen cases for the optimal spherical packing of circles has a density
of 0.75. There are only twelve unique solution sets for the optimal spherical
packing of circles upon the surface of a sphere. They are determined by
a unit arc-radius of sixty degrees and the twelve factors of sixty.
The solution sets that are derived from the twelve factors of sixty
are the geometric reason a circle is divided into 360 degrees and for the
Sumerians' choice of a base sixty system. When the radius of
the circle is one degree, 10,800 circles are an optimal spherical packing
of circles upon the surface of the sphere and each of the thirty faces
of a truncated spherical rhombic triacontahedron has an optimal spherical
packing of 360 circles per face.
The
Sumerians used a counting system of base ten for their daily commerce
transactions, just as we do today [6]. This
fact and the manner in which the sexagesimal system is presently used,
suggests the following hypothesis. The sexagesimal system is unique
to the geometry of the sphere developed by the Sumerians from their knowledge
of the twelve unique solution sets for the optimal spherical packing of
circles.After five thousand years, portions of the Sumerians' sexagesimal
system are still in use today. We use their base sixty system for
astronomy,
cartography, navigation, surveying, and timekeeping. When time
is thought of as a transformation of the earth's orientation with respect
to the sun, then all of the above arts are aspects of their geometry.
Hilbert's 14th problem is considered next and later, the first half of
the problem is solved for systems with integer solutions. The solutions
for fractional parts must wait for a future paper.
2.
THE 14th PROBLEM OF HILBERT. We
now state the 14th problem in the form of a theorem using Hilbert’s
own words in order to clarify what is to be proved.
THEOREM
2.1. "Let a number m of integral rational functionsX1,
X2,...,Xm of the n
variables x1, x2,...,xn
be given,
X1
= f1(x1,...,xn),
X2=
f2(x1,...,xn),
(S)
............................,
............................,
Xm
= fm(x1,...,xn).
Every
rational integral combination of X1,...,Xm must
evidently always become, after substitution of the above expressions, a
rational integral function of x1,...,xn. [Nevertheless,
there may well be rational fractional functions of X1,...,Xm
which, by the operation of the substitution S, become integral functions
in x1,...,xn.] Every such rational
functions of X1,...,Xm, which becomes integral
in x1,...,xn after the application of the substitution
S,
I propose to call a relatively integral function of X1,...,Xm.
Every integral function of X1,...,Xmis evidently
also relatively integral; further the sum, difference and product of relative
integral functions are themselves relatively integral." [4]
Let the existence of such a finite system be provided by the group GfPn,
with
the form Z2,...,Zn, where Z2
= ±1, and p = 2. A positive example result when Xm
= 8, 64, 4096 and with xn = 3, 6, 12 respectfully.
The
problem is to now demonstrate the existence of such "a finite system
of relatively integral functions X1,...,Xm,
by which every other relatively integral function of X1,...,Xm
may be expressed rationally and integrally." The idea of a finite
field of integrality is expressed by a system of functions from which a
finite number of functions can be chosen, in terms of which all other functions
of the system are rationally and integrally expressible. Further,
we desire that these integral functions f1,...,fm
have coefficients that are integers and included among the relatively
integral functions of X1,...,Xm only such
rational functions of these arguments as they become, by the application
of the substitution S, rational integral function of x1,...,xn
with rational and integral coefficients. [4]
In
order to prove this theorem, we must first construct the tetrahedral example,
demonstrate its ability to be extended, and then show that the extension
field is Abelian. The proof that the system is finite is inherent in the
geometric choice of the representations (the tetrahedron and its extended
family). The groups that define the regular polytopes are well known closed
finite systems. [3a]
3.
THE CONSTRUCTION OF THE EXAMPLE. We build the first point field
from a tetrahedron and its complex of unitary orthogonal vectors that compose
the group Z2,Z2,Z2.
THEOREM
3.1. Let X0, X1, X2,...,Xn-1
be a collection of unitary, orthogonal Tetrahedral-vectors, represented
by a diagonal matrix, of the Abelian rotational group Z2,Z2,Z2,
or Gf8. Then, these six T-vectors define
the rotational field for the six midpoints of the tetrahedron's edges.
The
matrix represents an orientation of the tetrahedron with respect to I,
an observer. The observer is introduced and represented by
the identity element, I (+1,+1,+1), and conjugate, -I (-1,-1,-1)
that together define an axis of orientation for the observer. The identity
element defines an absolute direction for up, upon which
all observers must agree. Furthermore, let each matrix represent a permutation
of this collection of six orthogonal T-vectors that may be thought
of as rays emanating from the center of the tetrahedron, passing through
the midpoints of the edges, and tracing the midpoints’ projection upon
the surface of a hyper-complex sphere. Therefore, the
group of elements Z2,Z2,Z2 and
the hyper-complex sphere may be extended to Gf’PnXGfPn
and/or GfPn+n, with the form Z2,...,Zn,
where Z2 = ±1, P = 2, and n+n = 2n, by
the action of multiplication and/or addition when the value for n
= 3, 6, 12. Figure 3.2 illustrates the idea of a tetrahedron
projected upon a hyper-complex sphere created by theorem 3.1.
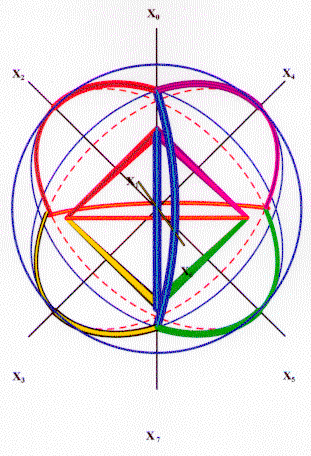
Figure 3.2
X0
= (+1,+1,+1); X1 = (+1,+1,-1); X2 = (+1,-1,+1); X3
= (+1,-1,-1),
X4 =
(-1,+1,+1); X5 = (-1,+1,-1); X6 = (-1,-1,+1); X7
= (-1,-1,-1).
We
next develop the algebraic space with the following theorem and corollaries.
THEOREM
3.3. The hyper-complex sphere Gf’PnXGfPn,
on whose surfaces an incident geometry is defined, is determined over the
sphere's finite point field by the following condition,
Gf’PnXGfPn
= [x e Gf’PnXGfPn]
| x2 = I,
with
the surfaces of the hyper-complex sphere the loci of all points, the distance
I
(+1,...,+1) an arc-radius of 60 degrees, from a given central
point.
COROLLARY
3.4. A great circle of 360 degrees is the locus of all points
the distance I, an arc-radius of 60 degrees from a given
central point, and coplanar with a hyper-complex plane incident to the
given central point.
COROLLARY
3.5. Diametrically opposite points that are separated by an arc of
180
degrees are conjugate points. When conjugate points are multiplied
together, the result has the form (-1,...,-1).
COROLLARY
3.6. Two points that are separated by an arc of 90 degrees are
perpendicular points. Two unit vectors from the given central point to
these points are perpendicular vectors. When perpendicular points are multiplied
together, the result is their pole point, another perpendicular
point, separated from the first two points by arcs of 90 degrees.
On
the surface of a three-sphere, a point is determined by three parameters,
Z2,Z2,Z2.[4b]
When any element defining a point, is multiplied by itself, the result
is equal to the identity element, I. The unitary three-sphere
encompasses an invariant volume of space. One must now confront the
chiral property of space, because modeling objects in space results in
both left-handed and right-handed variations. Our next task is to establish
the mathematical method to model both fields with one unified chiral field
and to demonstrate the concept of extension presented in the following
analysis of invariant forms.
4.
CHIRAL ISOMORPHISM AND DUAL TETRAHEDRAL GROUPS. In nature there
exist objects which, in all respects, are identical, except for their six-dimensional
spatial orientations. This chiral property is known as handedness or enantiomorphous,
and the difference between a person's two hands best represents the concept.
We model this idea mathematically over the hyper-complex sphere, which
accommodates simultaneous mapping of interrelated systems of coordinates.
The hyper-complex sphere is defined by Gf8 over the outside
surface of a three-sphere. Augmented by Gf’8 that is
defined on the inside surface, a spherical bubble models the six-dimensional
hyper-complex sphere, as a two-sided membrane.
A
mirror demonstrates the inversion of Gf8 and the dual
vector field Gf’8 is created. The left-handed system
of coordinates Gf’8 is defined by the tetrahedron in
the mirror. The right-handed system of coordinates Gf8
is defined by the original tetrahedron Gf8. The familiar
vector field is now labeled with unitary diagonal matrices that commute.
The spherical tetrahedra are illustrated in Figure 4.1.
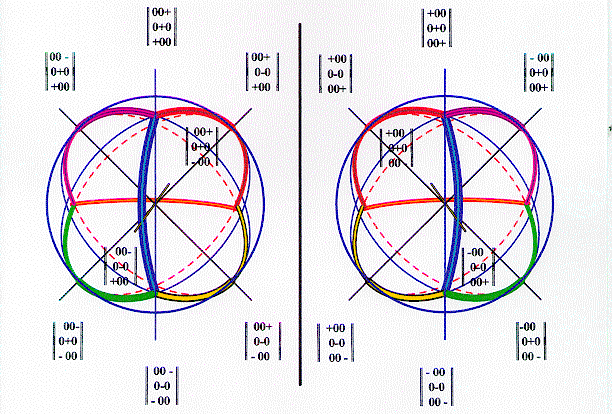
Figure 4.1
In
the dual vector field, the left-handed tetrahedron, is isomorphic to the
field of the right-handed tetrahedron. In the field of the left-handed
tetrahedron, the matrices are those of the secondary diagonals. The matrices
are converted into matrices with main diagonals by exchanging their first
and last columns. In all cases, this action produces negative matrices.
When multiplied and/or added together, they form the group Gf’8XGf8,
and/or Gf64, which has the form (-Z2,-Z2,-Z2
+ Z2,Z2,Z2). The group is Abelian,
of order Pn+n, and type (Z2,...Z2),
where Z2 = ±1, P = 2, and n+n=
6. The group Gf’8XGf8, demonstrates the
first example of extension into the new group Gf64. We
now prove theorem 3.1 for the algebraic extension field in
the general case.
Proof
of theorem 3.1: Following Weyl's [8] treatment of the transformation
of the principal axis, our proof uses the method of mathematical induction
over the familiar vector field. We seek a normal coordinate system ei,such
that in addition to
r = x1e1 + x2e2
+ ... + xnen
r2 = x21e21
+ x22e22 + ...
+ x2ne2n
(4.2)
we also have
A(r)
= a1 x21e21
+ a2x22e22
+ ... + anx2ne2n.
(4.3)
That
is, A will be brought into normal form 4.3 by means
of a multiplicative unitary transformation. An invariant correspondence
of the field upon itself is also referred to as a rotation or transformation
of the principal axes. The real numbers a1,
a2,...
, an
are called the characteristic numbers of the form A,
and e1, e2,...,en are the
corresponding characteristic vectors.
We
consider the correspondence r - r'= Ar
and seek those vectors r ¹
0, which are transformed into multiples r' =
l
r
of
themselves by A. We thus obtain the well known "secular
equation"
f( l
) = det( l
1 - A) = 0,
(4.4)
for
the multipliers l.
Then according to the fundamental theorem of algebra, this
equation certainly has a root l
= a1,
and there exists a non vanishing vector r = e1,
which satisfies the equation Ae1 = a1e1.
On multiplying this vector by an appropriate numerical factor so chosen,
such that its modulus is unity. Then, e1 may be
supplemented by n - 1 further vectors, e2 ,e3
,..., en, in such a manner that these n
vectors then constitute a normal coordinate system. In these coordinates,
the formula
ei'
= Aei = S
k
akiek
(4.5)
for
the correspondence A requires, in accordance with the definition
on e1, that the following coefficients a21,a31,...,an1
must vanish and a11 =
a1,
and because of the symmetry conditions aki = aik,
the coefficients a12,a13,...,a1n
must also vanish. Hence, in the new coordinates, the matrix A
takes the form
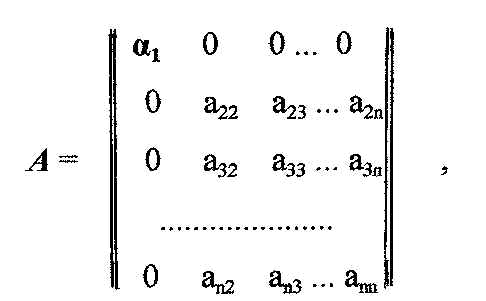
and
the modified hermitic form becomes
A(r) = a1x21
+ A'(r), (4.6)
where
A'
is the modified form containing only the n - 1 variables
x2,x3,...,xn. Repeating this process,
we establish the validity of theorem 3.1. The characteristic polynomial
of equation 4.3 is
det( l
1 - A) = ( l-
a1)(
l-
a2)...(
l-
an).
(4.7)
Thus
it follows that the characteristic numbers, a1,a2,...,an,
are uniquely determined, and their sum is the trace of A.
[8]
Since
these fields are discrete, we again verify theorem 3.1 with a computer
program that uses an algorithm to examine each possible permutation of
Pn,
which has the form Z2,...,Zn, where Z2
= ±1, P = 2, and n = 3, 6, 12. Using this notation,
we are able to demonstrate that the symmetric group of six variables is
solvable, when they are transformed, first into triplets, and then sextuplets.
[7a]
The
elements of the mirror image do not form a group. They do form a semi-group,
however, that divides the group in half. The group properties return to
the mirrored elements, when their complex conjugate identity operator(-1,-1,-1,+1,+1,+1)
is included in the algebraic law of multiplication. In the next section,
we use the above extension of liner algebra to demonstrate that the full
symmetric group S6, which is directly related to general
equations of the sixth-degree, is solvable over the finite field of the
regular polytopes.
5.THE
GENERAL N-TH DEGREE EQUATION. According to Galois theory, equations
of the n-th degree are not solvable by radicals when n is
greater than or equal to five. The following theorems use a linear algebraic
extension of matrices to provide the building blocks for the finite point
field of Gf’8XGf8. Using linear algebra and
group theory, we develop a form of algebraic geometry that allows the problem
to be solved over a discrete spherically symmetric point field when n=
3, 6, 12. These solutions, however, do not provide a counter example
to Galois theory of equations because they are not a radical form and they
do not provide a general solution. We simply eliminate the need to use
the radical form for the following existence proofs. Sets of algebraic
systems of functions do exist, when n = 3, 6, 12, that furnish integer
solutions for the coefficients of polynomial equations of degree n,
when defined by a known finite geometric set of polytopes.
DEFINITION 5.1.
A polynomial over a field F in the indeterminate value x is expressed by
an equation, such that
f(x) = c0xn
+ c1xn-1 + ... + cn-1x + cn
= 0,
where c0,
c1, c2,...,cn are elements of F called
coefficients of the polynomial.
Integral
functions, as polynomials are sometimes referred to, are completely determined
by their coefficients. Polynomials are monic when the leading coefficient
is equal to one, c0 = 1. Unitary solution sets result
if the last coefficient is equal to one, cn = ±1,
which
restricts the problem to the surfaces of a hyper-complex sphere. [2]
THEOREM
5.2. A function f(x) = 0 is solvable by algebraic extension, if and
only if G is a solvable group. Furthermore, let the group G
be equal to Gf8 and the extensions Gf’PnXGfPn,
with
the form Z2,...,Zn, where Z2
= ±1, P = 2, and n = 3, 6, 12.
Proof:
The finite group GfPn is solvable if there
is a sequence of consecutive subgroups, which start with the full group
GfPn
and ends with a subgroup that contains only the identity I. In the
decomposition chain, each subsequent subgroup is contained (Émeans
"contains") in the preceding one as a subgroup of index two, such that
GfPn
= GnÉ
Gn-1É
Gn-2É...É
G0= I,
for
a, such that 1 £
a < n, Ga is normal in Ga+1,
and the ratio [Ga+1 : Ga] is prime.
Since
the full symmetric group S6 is isomorphic to Z2,Z2,Z2,Z2,Z2,Z2,
all that remains is to show that Gf26 decomposes
into various subgroups as required above. The order of each subgroup is
2n with n = 0, 1, 2, 3, 4, 5, 6 and the decomposition
series is given, such that
Gf26 = 64 É
32 É
16 É
8 É
4 É
2 É
1.
Figure
5.3 is a mirror symmetric representation of the group Gf26
and/or Gf64, which illustrates the first decomposition
into two thirty-two element subgroups (the red and the blue fields). The
original pair of chiral tetrahedra are highlighted. The horizontal field
represents the left-handed tetrahedron and the vertical field represents
the right-handed tetrahedron.
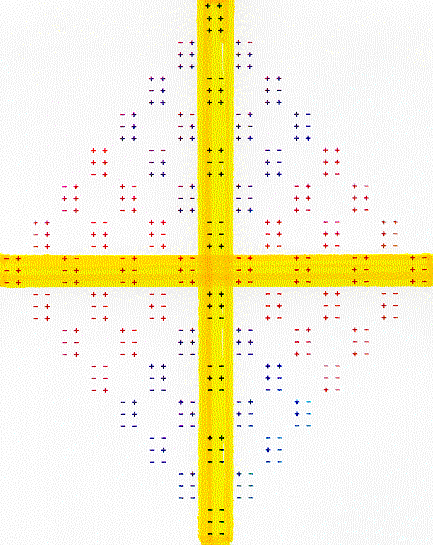
Figure 5.3
Table
5.4 displays the subgroups that Gf26 decomposes
into and the various regular polytopes that they represent.
| ORDER |
n
EQUAL |
REPRESENTATION
Gf2n |
| 64 |
6 |
The
group Gf64 |
| 32 |
5 |
Icosahedron-Dodecahedron
dual space
[the
icosahedron is represented by the blue elements
and the dodecahedron
by the red elements in Figure 5.3.] |
| 16 |
4 |
Octahedron-Hexahedron
dual space
[(++++++),(-++-++),(+-++-+),(-
-+- -+),
(- - - - -
-),(+- -+- -),(-+- -+-),(++-++-),
(-
- -+++),(+- - -++),(-+-+-+),(++- - -+),
(+++- - -),(-+++-
-),(+-+-+-),(- -+++-)] |
| 8 |
3 |
Tetrahedron
dual space
[(++++++),(-++-++),(+-++-+),(-
-+- -+),
(- - - - -
-),(+- -+- -),(-+- -+-),(++-++-)]
(-
- -+++),(+- - -++),(-+-+-+),(++- - -+),
(+++- - -),(-+++-
-),(+-+-+-),(- -+++-)] |
| 4 |
2 |
Kline
four group (+1, -1, +i, -i)
[(++++++),(-
- - - - -),(- - -+++),(+++- - -)]
Alternate
group
[(++++++),(-++-++),(+-++-+),(-
-+- -+)] |
| 2 |
1 |
Identity
and conjugate (+1,-1)
[(++++++),(-
- - - - -)] |
| 1 |
0 |
Identity
(+1)
[(++++++)] |
Table 5.4
We
now use these solvable groups to prove theorem 2.1 (for the integer
solutions to the 14-th problem of Hilbert) by demonstrating that all the
coefficients to the polynomial equations are integers.
Proof
of theorem 2.1 for n = 6, 12: Let the coefficient of the polynomial
c0, c1, c2,...,c6 be quantities,
which are algebraically independent over k. Set K = k(c0, c1,
c2,...,c6) and as before, define the f(x), such that
f(x) = c0x6
+ c1x5 + ... + c5x + c6Î
Gf26
is
the general equation of degree 6 over k. Suppose, f(x) = (x - x1)(x
- x2)...(x - x6) [isomorphic with equation
(4.7)] is in some extension field of F[Gf26].
It should be clear that the Xm are permutations of the
solutions to the equation, when Xm = fm(x1,...,x6).
It is not difficult to show that the x1,...,x6 are
algebraically independent over k. The proof of this establishes theorem
3.1
as shown above. Finally, the coefficients ci are elementary
symmetric functions of the xi, which are related to the
polynomials by the following equations,
c0 = 1 (a monic polynomial),
c1 = x1 + x2 + ...x6 (the trace),
c2 = x1x2 + x2x3
+ ... + x5x6,
c3 = x1x2x3 + x2x3x4
+ ... +x4x5x6,
...,
c6 = x1x2...x6.
[2]
The
proof is completed by substituting the various permutations of Xm
= fm(x1,...,x6), for the unitary values
of x1,...,x6, into the above elementary symmetric
functions of the xi and generating the coefficient of
all the equations of degree six in the solution set. The result is a demonstration
that the coefficients are all integers and that each possible permutation
satisfies the theorem. The 64 examples for degree six and the 4096 examples
for degree twelve are presented in Appendix
A .[7a] The group
of permutations for degree twelve is demonstrated in the same manner and
represented geometrically by the semi-regular polytopes. The example for
degree three is now presented.
Proof for n = 3:
let n equal three and substitute the permutations of Xm
= fm(x1,x2,x3), into the given
equations for the coefficients,
c0
= 1,
c1
= x1 + x2 + x3 (the trace),
c2
= x1x2 + x2x3,
c3
= x1x2x3,
and
solve the equation for the polynomial functions,
f(xi)
= c0x3 + c1x2 + c2x
+ c3 Î
Gf8,
using
the unitary permutations of Xm = fm(x1,x2,x3),
such that
X0
=(+1,+1,+1), X1=(+1,+1,-1), X2 =(+1,-1,+1), X3
=(+1,-1,-1),
X4
=(-1,+1,+1), X5 =(-1,+1,-1), X6 =(-1,-1,+1), X7
=(-1,-1,-1).
The
following solution set of polynomial equations are generated when Xmis
eight and xn is three,
X0 =(+1,+1,+1) = f(x0) = x3 + 3x2
+ 2x + 1 = 0,
X1 =(+1,+1,-1) = f(x1) = x3 + x2
- 1 = 0,
X2 =(+1,-1,+1) = f(x2) = x3 + x2
- 2x - 1 = 0,
X3
=(+1,-1,-1) = f(x3) = x3 - x2 + 1= 0,
X4 =(-1,+1,+1) = f(x4) = x3 + x2
- 1 = 0,
X5 =(-1,+1,-1) = f(x5) = x3 - x2
- 2x + 1 = 0,
X6 =(-1,-1,+1) = f(x6) = x3 - x2
+ 1 = 0,
X7 =(-1,-1,-1) = f(x7) = x3 - 3x2
+ 2x - 1 = 0.
In
dimension three, the algebraic and geometric system furnishes a positive
example for the existence of a finite system of functions having integers
for coefficients.
6.
THE IDENTITY ELEMENT AND THE OBSERVER. Previously we demonstrated that
the mirror image forms a semi-group, requiring its identity operator to
be included in the algebra. The observer was introduced and defined by
theorem 3.1 with the identity operator, (++++++), again shown
in its abbreviated form. The observer may change orientation with respect
to an object. For example, one may move around behind the object, which
is a change of 180 degrees. Therefore, the observer's operator changes
to its conjugate, (- - - - - -). When the observer's operator, defining
the observer's orientation, is included in the law of multiplication, the
result is a description of the object as seen by the observer. With this
idea in mind, the algebra is a natural consequence of the observers' viewpoint.
When
n
= 2, the polynomial equations have the form
c0x2
+ c1x + c2 = 0,
they define a great
circle around a hyper-complex sphere, which has only four solutions. The
solutions are the four invariant Gaussian numbers, +1, -1, +i, -i,
and defined respectfully for dimensions two and six by
(+1,+1), (-1,-1),
(-1,+1), (+1,-1);
(+1,+1,+1+1,+1,+1),
(-1,-1,-1,-1,-1,-1), (-1,-1,-1,+1,+1,+1), (+1,+1,+1,-1-1,-1,).
Theorem
3.1
physically place an observer into the mathematics by defining an orientation
of an object from the observer's perspective. The kernel identity
subgroup
of Gf64 is
(++++++),
(- - -+++), (- - - - - -), (+++- - -),
the
four identity operators. The circle of the solution set defines a hyper-plane
that divides the hyper-complex sphere into four sections. The observer,
who is defined by the operator (++++++), sees the circle
with a vertical set of diametrically opposite points, (++++++) and
(-
- - - - -). The observer, who is defined by the operator (- - -+++),sees
the circle with a horizontal set of diametrically opposite points,
(-
- -+++) and (+++- - -).
The
mirror image of a tetrahedron is defined on the inside of the hyper-complex
sphere. An observer defined on the outside of the sphere cannot see
this tetrahedron. Therefore, the complex conjugate identity operator, (-
- -+++), defines the observer on the inside of the hyper-complex
sphere. In this manner, the left-handed field is specified and all rotations
of the left-handed tetrahedron may be determined without the multiplication
changing its field. Three negative numbers multiplied together obviously
results in a negative number. In other analysis, the concept of absolute
value is introduced to restrict the results to the positive field, but
unlike other analysis, the choice of which field the observer is in determines
the correct value in this analysis.
The
use of the identity element to introduce an observer into the mathematical
structure of this analysis is the most important aspect of the paper. A
geometric interpretation for the identity element is an algebraic expression
for an observer's viewpoint of an object and the ability to express this
viewpoint in relation to the observer’s long axis. The mathematics is significant
because it is able to keep track of an object’s orientation and the orientation
of the observer viewing the object. The object’s final orientation, as
seen from the viewpoint of the observer, is described by the algebra after
rotating the object, the observer, or both over the surfaces of the hyper-complex
sphere.
7.
THE ALGORITHM FOR THE NUMBER OF CIRCLES IN THE OPTIMAL SPHERICAL PACKING
OF CIRCLES AND THE RESULTING POLYTOPES FOR THE SOLUTION SETS. We desire
an algorithm that generates different values for the number of circles
in a solution set for the optimal spherical packing of circles. The different
numbers represent larger and larger regular systems of points on the surface
of a sphere. With the knowledge that a circular covering problem is related
to the formula for the surface area of the sphere, we start with the formula
A
= 4 pr2.
For almost three thousand years, the Sumerians and their decendents used
two values for Pi, one of which was three.
It seems absurd that they would use such a poor value for such a long period
of time, unless one considers our beginning hypothesis. The sexagesimal
system is unique to the geometry of the sphere developed by the Sumerians
from their knowledge of the twelve unique solution sets for the optimal
spherical packing of circles. On the surface of a sphere, straight
lines are arcs of great circles and the ratio of twice the arc-radius
to the circumference of the great circle is three. A plane
illustration of a system without straight lines is shown in Figure 7.1.
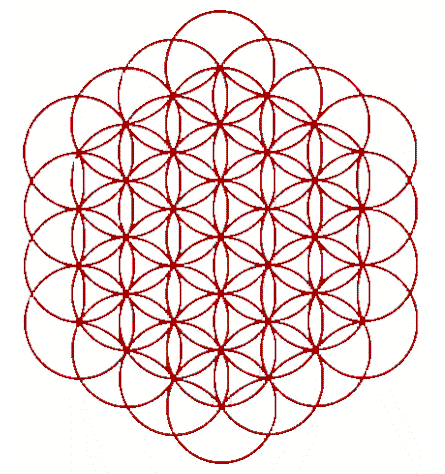
Figure 7.1
Therefore, we use
the surface area formula to generate the integer number of circles
on the surface of a sphere when Pi is three and the
variables for the circles diameters are divisions of the arc-radius. The
divisions of the arc-radius that provide integer solutions are the twelve
factors of sixty. The reason for our ancestors' choice of a
sexagesimal system based on the number sixty is the fact that only these
twelve numbers, the twelve factors of sixty, provide integer solutions
(modulo 60) for the optimal spherical packing of circles. The twelve
sets of the optimal spherical packing of circles, modulo 60, on
the surface of a unit sphere are given once again,
12(60); 48(30);
108(20); 192(15); 300(12); 432(10);
1,200(6); 1,728(5);
2,700(4); 4,800(3); 10,800(2); and 43,200(1).
The
integers in parentheses are the diameters of the circles in degrees. Since
we define the hyper-complex sphere as a two sided membrane, there would
also be twelve solution sets that are on the inside surface for a total
of twenty-four sets. Is this the geometric reason for the division of the
day into twelve and twenty-four hours? The algebraic and geometric
facts about the optimal spherical packing of circles are the reasons why
a circle is divided into 360 degrees and why the Sumerians and their
decendents persisted in their use of three for Pi.
When
the centers of the circles are considered as vertices they define two families
of polytopes. The representation fields for the optimal packing of circles
are old and new families of polytopes. The largest polytope, modulo
60, is a truncated rhombic triacontahedron with 44,132 faces,
43,200 vertices and 87,330 edges. The family of the truncated rhombic triacontahedron
has two additional members. The second family is the ten polytope family
of the truncated rhombic dodecahedron and the optimal spherical
packing of circles for the smallest polytope in the group is the cuboctahedron.
Appendix B[7b]
provides a detailed description
of each polytope in descending order based on their size and family. The
cuboctahedron is the first polytope in our extension fields to have its
vertices defined by rational whole numbers. The polytope is related to
the hexahedron (cube) by the fact that its vertices are the midpoints of
the cube's edges. The V4 vertices of its dual, the rhombic dodecahedron,
are the center of the cube's faces, which are determined by the crossing
of the perpendicular edges of a chiral pair of dual tetrahedra that are
coincident at their midpoints.
8.
CONCLUSIONS AND QUESTIONS. Theorem 2.1 was stated in the exact
words of Hilbert [the bracketed section] although not proved, was left
in. The reason for this is the extension to our algebra, which proves the
bracketed section, also extends the field of the hyper-complex sphere to
include the rational fractional functions of X1,...,Xm
which, by the operation of the substitution S, become integral functions
in x1,...,xn. Therefore, the completion of
this proof [the bracketed portion] and the geometric proof for the group
Gf212
must wait for additional papers. Additional proofs for the theorems and
the generation of the algebraic examples, 64 for Gf26
and 4096 for Gf212, are demonstrated in Appendix
A.Since the field is
finite, proof is by exhaustion with the algorithm examining all permutations.
Corollary 3.6 is proved with the geometric proof for the group Gf212
in a future paper.
We
accomplished the goal of constructing positive examples algebraically
and geometrically by the combination of simple yet invariant geometric
forms, which create higher forms. Using the ideas of a field and a group,
the regular polytopes are constructed in an algebraic fashion with a tetrahedron
over Gf8, a pair of chiral tetrahedra over Gf’8XGf8
(which
combine to form a hexahedron), and all of the regular polytopes over Gf64
by the addition of the various subgroups.
We again note that the
group Gf64 is the master rotational group for the regular
polytopes.
The
group of 64 hyper-complex numbers defines dual orthogonal subgroups. When
these subgroups are mapped to a spherical tessellation of an icosahedron,
thirty-two of the numbers are found on each side of the membrane. Thirty
are found at the midpoints of the tessellated edges. Two additional pole
points define the observer’s long axis and its relationship to the icosahedron.
The dodecahedron, the dual of the former, is mapped to the inside surface,
with its thirty edges orthogonal to its dual. The dual polytopes midpoints
for the two sets of edges are coincident to each other, but on opposite
sides of the membrane.
When
the group Gf64 is extended by multiplication, Gf’64XGf64
defines geodesic lines. Sets of these geodesic lines are then used to reconstruct
the regular polytopes on the same surface. Gf’64XGf64
defines 128 pairs of perpendicular points out of 4096 possible permutations.
In the proof of corollary 3.6, how are these 128 pairs of perpendicular
points determined? The theorem of Lagrange is considered as a theorem of
composition. [1] The algebraic extension (composition) to Gf’8XGf8,
and/or
Gf64
creates ten tetrahedra. The ten tetrahedra are the various finite geometrical
subgroups, into which Gf64 decomposes and by which the
regular polytopes are constructed (composition). We have just shown by
theorems 3.1 and 5.2 that the Abelian group Gf64
manifests both of these properties (composition and decomposition). We
ask the following questions: What are the subgroups, including their identity
operators? Define the right-handed tetrahedra (there are five), the octahedra
(there are five), and the icosahedron on the outside surface. Then define
the dual for each of the above polytopes on the inside surface of the hyper-complex
sphere. These questions will be answered in a journal published paper.
Meanwhile, we offer the above questions as a challenge, to again stimulate
research into hyper-complex numbers. The correct answers should follow
the format presented in this paper with the unitary value of each sign
understood, such as
T1(++++++)[(++++++),(-++-++),(+-++-+),(-
-+- -+),
(- - - - - -),(+- -+- -),(-+- -+-),(++-++-)].
In
addition, there are four more tetrahedrons, T2, T3,
T4,
and T5.
T'1 (- - -+++)[(- - -+++),(+- - -++),(-+-+-+),(++- - -+),
(+++- - -),(-+++- -),(+-+-+-),(- -+++-)].
In
addition. there are four more tetrahedrons, T'2, T'3,
T'4,
and T'5. When H stands for the hexahedron or cube,
we have
H1(-
- -+++)[(++++++),(-++-++),(+-++-+),(--+--+),
(- - - - - -),(+- -+- -),(-+- -+-),(++-++-),
(- - -+++),(+- - -++),(-+-+-+),(++- - -+),
(+++- - -),(-+++- -),(+-+-+-),(- -+++-)].
In
addition, there are four more hexahedra, H2, H3,
H4, and H5. When O stands for the
octahedron, we have O1 ....
Hint,
Figure 5.3 is mirror symmetric and the group Gf64
decomposes into mirror symmetric subgroups similar to Figure 5.3.
Therefore, one should also submit a set of mirror symmetric images that
portray the decomposition of the two groups in Figure 5.3 into two
groups that have five tetrahedra each as subgroups.
ACKNOWLEDGMENTS.
I
would like to thank Earl Halverson, of Billings, Montana, who taught complex
numbers, by having the class imagine the existence of the imaginary axis
on the backside of the blackboard. I thank Richard Crandall, at Reed College,
Portland, Oregon, for his time, patience, and critical review, which turned
my work into understandable articles. I thank Chris Radcliffe, the co-author
of Appendix A and Michael Ryals for their helpful suggestions. Finally,
I thank Welcome Lindsey for her applied expertise in technical writing.
REFERENCES
1.
R. Carmichael, Introduction to the Theory of Groups of Finite Order,
Dover Publications, Inc., New York, 1937, 120-354.
2.
A. Clark, Elements Of Abstract Algebra, Dover Publications, Inc.,
New York, 1971, 67-129.
3a.
H. Coxeter, Introduction to Geometry, 2nd Ed., John Wiley
& Son, Inc., New York, 1989, 148-159.
3b.
H. Coxeter, The Regular Polytopes, Dover Publications, Inc., New
York, 1971, 67-129.
4a.
D. Hilbert, Mathematical Problems*, Bull. Amer. Math. Soc., 8, 1902,
437-479, *Translated for the Bulletin, by Dr. Mary Winston Newson. The
original appeared in the Gottinger Gachrighten, 1900, pp. 253-297, and
Archiv der Mathematik and physik, 3d ser., vol. 1 (1901), pp. 44-63 and
213-237.
4b.
D. Hilbert and S Cohn-Vossen, Geometry And The Imagination, Chelsea
Pub. Co., New York, 1983, 52-93.
5.
M. Nagata, On The 14-th Problem Of Hilbert, Am. Journal Of Mathematics,
Vol. 81, 1959, 766-792.
6.
O. Neugebauer, The Exact Sciences In Antiquity, Dover Publications,
Inc., New York, 1957, 1-40.
7a.
J. Van Dyke, and C. Radcliffe, Appendix A, pending publication on
the Internet, upon publication of OPTIMAL SPHERICAL PACKING OF CIRCLES
AND HILBERT'S 14TH PROBLEM.
7b.
J. Van Dyke, and C. Radcliffe, Appendix B, pending publication on
the Internet, upon publication of OPTIMAL SPHERICAL PACKING OF CIRCLES
AND HILBERT'S 14TH PROBLEM.
8.
H. Weyl, The Theory of Groups and Quantum Mechanics, Dover Publications,
Inc., New York, 1950, 1-40.
Mathematics
Subject
Classification:
03C13, 11R20.
KEY WORDS:
master
Abelian rotational group, polytopes, Gf'PnXGfPn,
new families of polytopes, optimal spherical packing of circles, Mathematical
foundations, sexagesimal analytic geometry, unitary diagonal matrices,
elements, finite groups, Icosahedral, Octahedral, Tetrahedral, dual groups,
six-dimensional space, the 14th problem of Hilbert, nth degree
polynomials, spherical projection plane, Z2,Z2,Z2,Z2,Z2,Z2,
solvable group S6, matrix algebra, regular polytopes,
surface of a hyper-complex sphere, extension fields, chirality, invariance,
unified commuting vector field, orthogonal rotational group.
VisMathHOME
|
|
|