|
Spiral Tilings Paul Gailiunas 25 Hedley Terrace, Gosforth Newcastle, NE3 1DP, England Abstract In Tilings and Patterns [1] Grünbaum and Shephard comment that there is extremely little literature on the subject of spiral tilings. They survey what is known, and leave some unanswered questions, in particular whether there is a tile that will produce an r-armed spiral tiling for any odd value of r ³ 5. A new method of generating tiles from regular polygons is developed here, that allows the construction of zig-zag spirals with any desired number of arms. Spiral tilings of a type already known are considered and new tilings, related to them, are described. Further new tilings are constructed by considering some special cases.
Zig-zag Spiral Tilings Overlapping copies of any regular n-gon
will produce a shape that will tile the plane (without gaps) in several
different ways, one of which is a one-armed spiral, along with various
two-armed spirals [2]. If n is odd it is difficult
to get much further, but if n is even then the tile that is produced
can be cut into a series of rhombuses (fig.1), ensuring
that each cut has the same length as a side of the polygon. Any one cut
divides the original tile into two new ones, both of which will tile the
plane in a variety of ways, in certain circumstances including spirals.
In an n-gon it is easily verified that the angles of the rhombuses
are an integer times 1/n turns (where 1 turn = 360°). In fact
the rth rhombus has an angle of r/n turns, so it is possible
to choose a cut that will produce a tile having one angle that is 1/m
turns, if m = n/r.
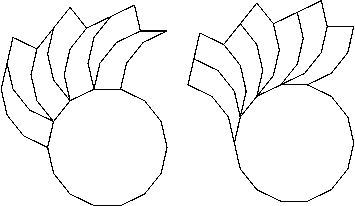
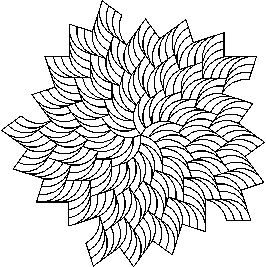
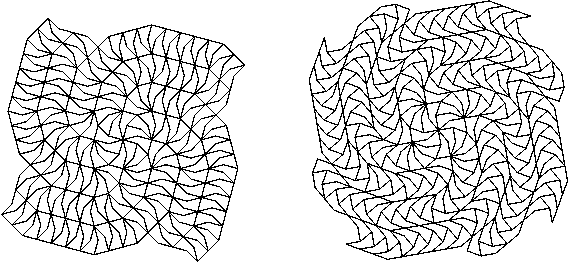
Figure 3: A five-armed
spiral from a tile based on a decagon. It has ten points.
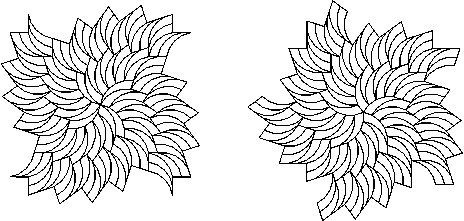
Figure 5: The same
tile from a 20-gon can be used to make a
The alternative way of tiling the spiral
arms, indicated in the fig.2 , will only work in two
cases, a three-armed spiral with a tile based on a dodecagon (fig.6)
and a four armed spiral with a tile from an octagon (fig.7)
. The reason is seen most easily in the three-armed example.
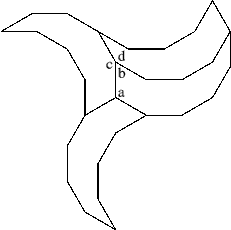
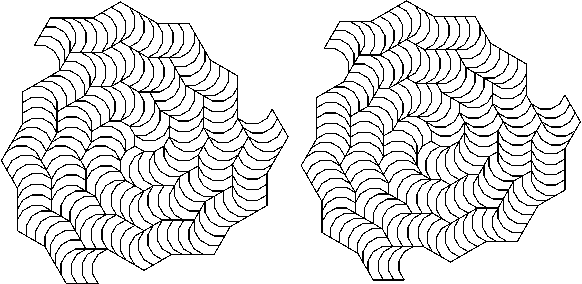
Figure 6: Two types
of three-armed spiral using a tile from the dodecagon.
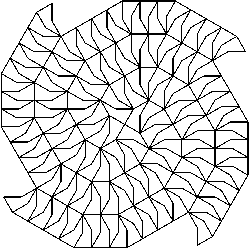
Figure 7: Two types
of four-armed spiral using a tile from the octagon.
Versatiles In the particular cases when n is a multiple of 6 one of the rhombuses will have an angle of 1/6 turn, and it can be seen as two equilateral triangles. (Actually there are two such rhombuses, but we are only concerned with the one having the angle of 1/6 on the convex side of the n-gon.) Making the cut that divides this rhombus into triangles generates a tile (fig.8) of the type discussed by Grünbaum and Shephard, and termed a versatile in their 1979 article [3].

Grünbaum and Shephard showed that
such tiles will always produce one-, two-, three- and six- armed spirals.
It is not clear whether they realised that all except the three-armed case
can be constructed using either tiling pattern i) or
ii). They certainly never mention it, and they use type ii) in only
one, a very attractive two-armed spiral (which is used on the dust-wrapper
of their book).
In the special case when n = 12,
the dodecagon, there are further possibilities. Like any versatile
it will produce several two-armed, a three-armed and the two types of six-armed
spiral. Rice and Schattschneider [4] have also described
some other ways that it will tile the plane. This particular versatile
also generates a four-armed and an eight-armed spiral. The four-armed spiral
(fig.10) is possible because the base angles of a versatile
are 1/6 turn (making the six-armed spirals possible) and (1/3-1/n)
turn (making the three-armed spiral possible, by combining a tile with
its mirror image). When n = 12, (1/3-1/n) = 1/4, hence
a four-armed spiral is possible. The only other value of n that
works to give an integer division of a full turn, n = 6, the hexagon,
gives a tile that is degenerate (an equilateral triangle).
Figure 10: A four-armed spiral using the dodecagon versatile.
The other possibility to consider is combining
the apex (of 1/n turns) with the 1/6 angle. The solutions of 1/n
+ 1/6 = 1/m must have m < 6, and m = 3 is the degenerate
case again. The case m = 4 has n =12, and a tiling (having
eight arms) is possible (fig.11), but the tiles produced
when m = 5 do not fit together in the same way, and there is no
analogous tiling based on a 30-gon.
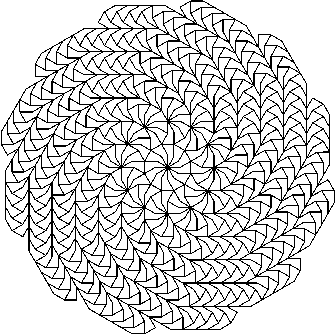
Figure 11: This tiling
shows particularly clearly that the spiral arms, of both
Rice and Schattschneider published this
tiling (fig.11) with arms of type i),
and again it is not clear if they were aware of the type ii)
alternative. They also mention the existence of a twelve-armed spiral using
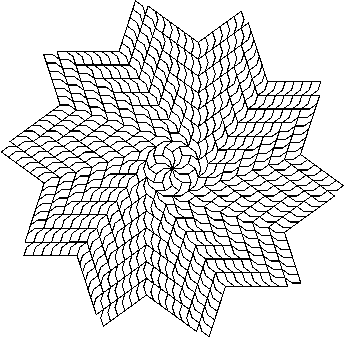
this tile. There are many variants of this tiling (fig.12
shows one of them), since there are several ways to construct the central
dodecagon. The next layer, which enlarges the dodecagon to twice its size,
can be constructed in many different ways, and the spiral arms themselves
can be of either type i) or ii).
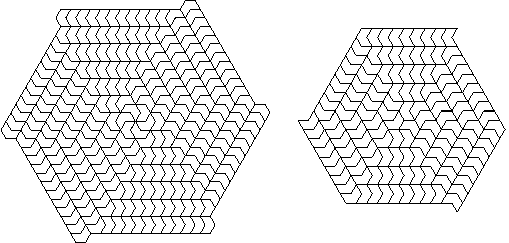
Figure 12: One of the many variants of a twelve-armed spiral using the dodecagon versatile. V-Shaped Tiles The arms of this spiral tiling (fig.12) can be seen as originating at the mid-points of the sides of the large dodecagon, with tiles fitting around its vertices. Clearly this is only possible if the tile has no more than two concave sides, and is more or less v-shaped. The only versatile with this characteristic is derived from the dodecagon, but such tiles can be formed from any polygon. The one from the hexagon is big enough this time to produce tilings that are recognisable as spirals. Spiral tilings made with this tile (fig.13) are probably the simplest that have more than two arms, and it is surprising that they are not mentioned in the existing literature on the subject.
It is always possible to cover an n-gon
of double size, using a tile derived from the n-gon, when n =
2(2r + 1), but only the decagon provides a v-shaped tile that
does this. It generates a ten-armed spiral (fig.14),
and of course in this case the arms are zig-zags.
Conclusion Tiles that are derived from regular polygons provide the most obvious possibilities for covering the plane in ways that that appear as spirals. Zig-zag spirals can be produced with any desired number of arms by following general methods, and versatiles provide smooth spirals, although only a limited number of arms is possible. Although many special cases have been considered, it is by no means certain that there are no more left to be found. Also the possibility of finding spiral tilings using entirely different types of tile, not based on regular polygons, has not been eliminated. Indeed some examples are discussed in [1], and, although further development along these lines seems unlikely, a different approach might produce more fruitful possibilities.
References [1] Grünbaum B. and Shephard G.C.,Tilings and Patterns, W.H.Freeman and Company, 1987. [2] Hatch G., "Tessellations with Equilateral Reflex Polygons", Mathematics Teaching, No.84, Sept.1978, p.32. [3] Grünbaum B. and Shephard G.C., "Spiral Tilings and Versatiles", Mathematics Teaching, No.88, Sept.1979, pp.50-1. [4] Rice M. and Schattschneider
D., "The Incredible Pentagonal Versatile", Mathematics Teaching,
No.93, Dec.1980, pp.52-3.
|