|
by Jay Kappraff* and Gary W. Adamson** New Jersey Institute of Technology, Newark, NJ, Kappraff@aol.com* , P.O. Box 124571, San Diego, CA 92112 - 4571** Abstract A hierarchy of rational numbers is
derived from the integers and shown to be related to naturally occurring
resonances. The integers are also related to the Towers of Hanoi puzzle.
Gray code is introduced as a tool to aid in understanding Towers of Hanoi
and also used to predict the symbolic dynamics of the logistic equation
of dynamical systems theory. The Towers of Hanoi and Gray code are both
generalized to number systems base n and used to derive a probability
density function for the divisibility of integers. The number system base
4 expressed in generalized Gray code is shown to be a natural framework
for the representation of the 64 codons of DNA. Finally, a
new algorithm is presented to compute the value of continued fractions
with repeating indices.
1. Introduction What do the divisibility properties of
the positive integers have to do with the Towers of Hanoi puzzle, Gray
code, dynamical systems theory, and the structure of DNA? This paper explores
these relationships.
2. A Natural Hierarchy of Numbers It is not commonly known that when one counts the positive integers one also counts a hierarchy of rational numbers, 0 < p/q < 1, in lowest terms in which the "most important" rational numbers appear higher on the list. Our meaning of "most important" will be defined below, but first we describe a procedure for determining location of a number in the hierarchy by giving an example. What is the 19th rational number in this hierarchy? To answer this, first write 19 in binary, i.e, 19 = (10011)2. Next duplicate the last digit and separate the contiguous 1s and 0s as follows: 1 00 111 corresponds to [1,2,3] where the numbers in brackets are the number of 1s and 0s in each contiguous group, i.e., 1 one, followed by 2 zeros, followed by 3 ones. The numbers in brackets are the indices of the continued or compound fraction expansion [1],[2] of the 19th rational number in the hierarchy, i.e., 19 corresponds to [1,2,3] =1/ (1+1/(2+1/3)) = 1/1+1/2+1/3= 7/10 Note that the boldface indices appear as elements of the continued fraction and that the second representation is a shorthand form of the first. Given its indices, the continued fraction can be rapidly evaluated by the procedure given in Appendix A. While continued fractions with a finite number of indices represent rational numbers, continued fractions with an infinite number of indices represent irrational numbers. However, if the sequence of indices for a rational number are repeated in a periodic manner, i.e., [a1,a2, ,an,a1,a2, an, ] = [a1,a2, an]¥ a special class of irrational numbers are generated, one for each rational number. These irrational numbers can be determined by a surprisingly simple algorithm based on generalizations of the golden mean due to Adamson and given in Appendix B. The following algorithm determines the rational number corresponding to any integer of the hierarchy. a) Write the number in binary. b) Duplicate the last digit and write the numbers of 0s and 1s in each contiguous group, referred to as the indices, beginning from left to right. c) These are the indices of the continued fraction expansion of the rational number in lowest terms, i.e., p/q = [a1,a2, ,an] = 1/a1 +1/ a2 + + 1/an Note that [a1,a2, ,an] = [a1,a2, ,an-1,1] for an>1. By duplicating the last digit of the binary notation we have chosen the first rather than the second representation. The procedure for determining the rational number corresponding to a given integer can also be carried out in reverse by using the Euclidean Algorithm to determine the indices of the continued fraction of a given rational number (see Appendix C), and then working backwards to the corresponding integer. Using this algorithm 1/2 = [2] corresponds to the integer 1 after eliminating the duplicated last digit. Therefore 1/2 sits atop the hierarchy. Table 1 lists the first 15 numbers in the hierarchy. In this Table, the 2n-1 integers with n digits are grouped in blocks and their corresponding rational numbers have continued fraction representations with indices that sum to n+1, e.g, there are 8 integers with 4 digits whose corresponding rationals have indices that sum to 5.
It should be noted that, strictly speaking, it is the blocks in Table 1 that are ordered in the hierarchy. Within each block there is no strict ordering of "importance," e.g., in block 4, 3/4 is no more "important" than 1/4, 3/5, or 2/5. The numbering of rational numbers within each block of Table 1 follows the well-known Farey sequence shown in Table 2 [2],[3], [4].
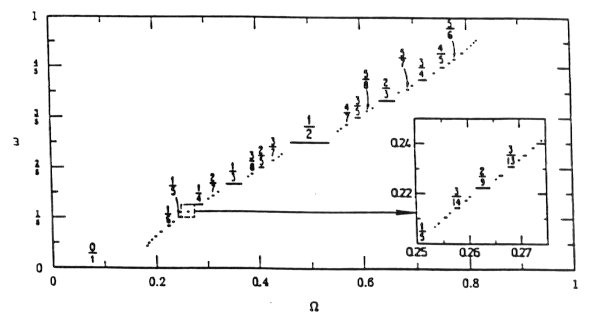
In this table each rational number is generated from the two that brace it from above by adding numerators and adding denominators of this pair, e.g., 5/8 is braced by 3/5 and 2/3 so that 5/8 = (2 +3)/(5+3) and 5/7 is braced by 2/3 and 3/4. Beginning in row 0 and counting right to left, we find that 5/8 is the 10th rational in the hierarchy. Applying the above procedure, 10 corresponds to 1 0 1 00 (with the last digit duplicated) which corresponds to the continued fraction [1,1,1,2] = 5/8. Continuing to the next row, you can check that 7/10 is indeed the 19th fraction in the hierarchy. It should also be noted that any term x in a row of the Farey sequence gives rise to two terms 1/(1+x) and x/(1+x) in the next row, e.g., x= 2/5 in row 2 gives rise to 5/7 and 2/7 in row 3. Figure 1 illustrates the so-called devils or satanic staircase generic to almost all dynamic systems [3]. This figure graphs the winding number w vs a frequency ratio W that represents the ratio of a driving force frequency and the resonance frequency of an oscillator for a system known as the circle map [3]. In this map a sequence of points z0 , z1, z2 are generated by the application of the function , zj+1 = R(zj) where R(z) = z + W - k/2p sin 2p z.
Figure1. Devils staircase with plateaus at every
rational number. From Fractals, Chaos and Power Laws by M.
The j indices can be thought of as time intervals. The winding number w of the map is defined as the limit of (zn-z0)/n as n®¥ . Map R depends on a parameter k related to the energy of the system. As k® 1, a critical value, the system approaches a chaotic state in which every winding number from the unit interval [0,1] is obtained depending on the value of W with rational values of w phase locked to finite intervals of W . By phase locking we mean that the same winding numbers are manifested for a finite interval of W values. The phase locked intervals for the irrationals have zero width and so the irrationals form a kind of "dust" between the rationals. We see that the higher a rational number is in the hierarchy the wider is the phase locked interval corresponding to it. Winding numbers represented by larger intervals correspond to resonances of dynamical systems with greater stability justifying our reference to the rationals corresponding to these intervals as being "more important." For example the three widest plateaus occur for 1/2, 2/3, and 1/3 corresponding to the first three rationals of the hierarchy. The relative widths of the plateaus are ordered according to the terms of the Farey sequence with elements within each row having approximately the same width. We make the following remarks about the relationship between the rational numbers in Table 1 and their continued fraction representations: a) The greater the sum of the indices the smaller the plateau widths. b) Within each block of Table 1 the continued fractions with the most dispersed series of indices occur for rational numbers that are the ratio of two integers from the Fibonacci series: 1 1 2 3 5 8 13 , e.g., when the sum of the indices equals 5 the most dispersed continued fraction indices occur for 5/8 and 3/8, e.g., 5/8 = [1,1,1,2] is highly dispersed in contrast to 3/7 = [2,3] , less dispersed. The ratio of Fibonacci numbers always appears at approximately the 1/3 and 2/3 positions of the integer block, e.g., for the integer block 8-15, ë1/3×8û = 2 and ë2/3×8û = 5 where ë û is the least integer function. Therefore the rationals 5/8 and 3/8 are positioned at 8 + 2 = 10 and 8 + 5 = 13 in the hierarchy. c) Other
widely dispersed index sets occur for the continued fraction representations
of ratios of integers whose numerator is from the Fibonacci series and
denominator is from the Lucas series. The Lucas series is the series: 1
3 4 7 11 18 29
, i.e., a series beginning with 1,3 in which each element
is the sum of the previous two. These continued fractions are located approximately
at the 1/6 and 5/6 positions in that segment of the table. For example,
in integer block 64 -127 (not shown) the positions 64 +ë5/6×64û
= 74 and 64 + ë5/6×64û
= 117 correspond to the rationals 21/29 = [1,2,1,1,1,2] and 8/29 = [3,1,1,1,2]
respectively.
3. Gray Code, Divisibility, and the Towers of Hanoi Notice that the strings of 0s and 1s (bit strings) in the third column of Table 1 are labeled as Gray code. Gray code is a system of representing integers as bit strings such that from integer to integer only a single bit changes in its representation unlike binary in which more than one bit can change from one integer to the next, e.g., 7 = 111 whereas 8= 1000. To go from one integer to the next in Gray code the value of the bit in the least significant digit changes (0 to 1 or 1 to 0) to give a bit string not already listed. Given the Gray code representation of an integer, the indices of the continued fraction corresponding to that integer can be obtained directly by a procedure given in Appendix D. The digits of the Gray code bit strings have been labeled 0,1,2, from right to left and the digit of the Gray code that changes is listed in column 4; it is the sequence, 0102010301020104 (1) Where does this sequence come from? Take the integers and divide a given integer by the highest powers of 2 that goes evenly into it and record the exponent of the highest power which we refer to as the index of the factor (see Table 3). If an integer is not divisible by 2 then its index is 0.
You will notice that Sequence 1 has made its appearance again. Now if you remove the 0s, or alternatively, add 1 to each term, you get another familiar sequence, 121312141213121 (2) This corresponds to the sequence of moves required to solve the Towers of Hanoi puzzle described below. Next reduce each integer in this series by 1 to get 010201030102010 a replication of Series 1. Of course this transformation (remove the zeros and reduce by one each of the remaining numbers in Sequence 1) can be repeated ad infinitum so that we have found a self-similar pattern within the number system related to division by 2. Note that if the modulus of any pair of adjacent numbers a/b and c/d in the Farey Sequence of Table 2 is defined to be |ad-bc|, then the Towers of Hanoi sequence is asymptotically developed for Row n as n®¥ . For example, the sequence of moduli for Row 3 of Table 2 is 3537353 which corresponds to 1213121 with the following replacements: 3®1, 5®2, and 7®3. The moduli of the first 15 entries to the Farey sequence are shown in column 5 of Table 1. The final idea in this cycle of ideas requires us to describe the Towers of Hanoi puzzle (abbreviated TOH). The Towers of Hanoi puzzle, an invention of the French Mathematician Edouard Lucas in 1883, is rich in number theoretic relations [2],[5],[6]. N disks of increasing sizes, numbered 1,2,3, ,N from smallest largest are placed on one of three posts (see Figure 2). The object of the puzzle is to move all the disks to another post in such a manner that a large sized disk never lies atop a smaller sized disk during the transfer. If the posts are labeled A,B,C in a clockwise manner and the first move is in a clockwise direction, then the shortest path to the final configuration is unique. The sequence of moves is shown in column 8 of Table 1. Here the configuration d1/d2/d3/ dm signifies that disk d1 lies atop disk d2 atop d3 etc., e.g., 1/2/3 means that disk 1 lies atop 2 which lies atop 3. 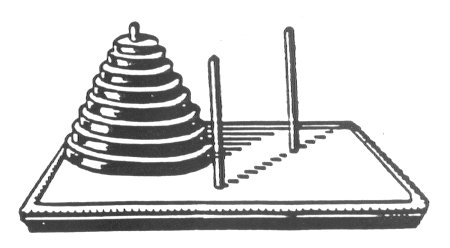
Figure 2. The Towers of Hanoi Puzzle with posts arranged in a circular fashion An optimal transfer satisfies the following rules: a) A smaller disk must always lie atop a larger disk; b) The parity of two adjacent disks must also be different, i.e., adjacent disks must be even odd or odd even numbered, e.g., in the example, 1 lies on 2 and 2 lies on 3 in the above example. c) During any transfer, an odd numbered disk moves clockwise (CW) while an even numbered disk moves counterclockwise (CCW). The puzzle begins with all the disks on post A as shown in Table 1. In subsequent moves, only newly transferred disks are indicated on post A. Observe that the TOH positions are correlated with the integers. In fact the following algorithm enables one to convert from the binary representation of the integer to a TOH position: a) For a given integer, express its binary representation in terms of its number of repeated digits. For example, 22 = 1 0 11 0 is written as {1121} since the initial 1 and 0 and the final 0 are singletons whereas the middle 11 is a pair. b) Starting
at the right, this set of indices describes how to uniquely place n
disks
onto the three TOH posts. The quantities of disks corresponding to the
first index are placed on a post in the order 1,2,3,
The number of disks
corresponding to the second index then go on another post.
Following these rules for {1121} the TOH position is : 5 2/3 1/4 Or, starting at the right, the first disk (#1) must go onto a post. Then the next two disks (#2 and #3) must go onto a different post. Then disk #4 must go onto a different post from the preceding one. However, according to rule c, we now have a choice: Vacant post or occupied post Always choose the occupied post as long a the parity rule is not violated. Therefore, #4 goes beneath #1. Then #5 must go onto a different post since it cannot go beneath disk #3 because of parity (no two odds together), so it must go onto the vacant post. In this manner, each integer n is uniquely associated with a TOH position. Let us now make a short digression to
convert a binary number directly to its equivalent Gray code representation.
Consider 19, represented in binary as 10011. Multiplying by 2 and adding
the next digit we get the sequence 1, 2, 4, 9, 19. These are the decimal
representations,
B19, of the family of binary numbers:
1, 10, 100, 1001, 10011. Next take the differences of adjacent terms of
the B19
sequence which we refer to as the Gray code sort,
Taking each number of the Gray code sort mod 2 (i.e., even is 0 and odd is 1) yields the Gray code equivalent, 11010. However, perhaps more significantly, the Gray code sort indicates the number of times the nth disk moved, up to the Nth move in the transfer to the final TOH position, e.g., up to the 19th move: disk 1 moves 10 times, while disks 2,3,4, and 5 move 5,2,1, and 1 times respectively. Binary numbers can also be converted directly to Gray code by Algorithm 3. a) Record the leftmost digit of the binary representation. b) If the k+1-th digit of binary is equal to or larger than the k-th digit then the k+1-th digit of the Gray code representation is the difference between these digits. c) If the k+1-th digit is less than the k-th digit, then add 2 (base number of binary) to the k+1-th digit, and then subtract the k-th digit from it to obtain the k+1-th digit of Gray code. For example, 1 0 0 1 0 ®
1 1 0 1 0
4. The Generalized Towers of Hanoi Problem We refer to the Towers of Hanoi puzzle
as TOH:2 because, as we have seen, it is based on the binary numbers. We
have been able to generalize this puzzle to the transfer of disks between
n+1
posts which we refer to as TOH:n. Once again the n posts
are arranged in a circular formation and a small sized disk must always
lie atop a larger disk. However, in any given move a disk can only move
to an adjacent post and, as before, we begin by moving the first disk clockwise.
For example, let us consider TOH:3 with four posts. Labeling the
posts A, B, C, D arranged in a clockwise fashion,
i.e., A ® B
® C ®
D ® A,
and beginning with two disks on post A, using the previous notation,
the following sequence transfers these disks optimally to another post:
This sequence of moves follows the pattern 1121. As before odd numbered disks move CW while even numbered disks move CCW. Also, on any post, adjacent disks must have different parities. The sequence of moves for the optimal transfer for TOH:n are again related to the exponent of the greatest power of n, referred to as the index, that divides evenly into a given integer. Table 4 illustrates the divisibility sequence for TOH:3.
Eliminating the zeros results in the TOH:3 sequence 112112 reproducing the sequence for the transfer of two disks described above, then continuing on. We can also determine the Gray code sort
corresponding to the n-ary, or base n, representation of
the number of moves N and use this to predict the number of moves
each sized disk makes during the optimal transfer. To do this express the
TOH:n position in the number system base n. For example,
step number 137 is represented in base 3 as (12002)3. The sequence
B137
in base 3 is then obtained by multiplying each digit of the binary representation
by 3 and adding the next digit to get: 1,5,15,45,137 which gives the decimal
values of the base 3 sequence: 1,12,120,1200, 12002. Next take the difference
to yield the Gray code sort:
Thus, disk 1 moves 92 times and disks 2,3,4,5 move 30, 10, 4, 1 time respectively. If the Gray code sort numbers are expressed mod 3 we get the generalized Gray code representation of 137 or 11102. We can get the generalized Gray code of integer N directly from the base n representation by slightly modifying Algorithm 3 so that in step c the base number n is added to the k+1-th digit if it is less than the k-th digit. Just as for Gray code, a single digit changes between successive integers represented by generalized Gray code and the place value of the change numbered 0,1,2, from the right represents the highest power of n that divides evenly into N. For example, expressing the following numbers in the base 4, 31 = (133)4 and 32 = (200)4 with Gray code representations, 31 = (120)4 and 32 = (220)4. Notice that a single digit changes in the third place (i.e., place value 2). Therefore 42 is highest power of 4 that divides evenly into 32. Also note that 31 mod 4 is gotten by adding the digits of the Gray code representation mod 4, e.g., 31 mod 4 = (1+2+0) mod 4 = 3. This holds for any integer N written in any base n. Table 5 lists the generalized Gray code for the first 64 numbers of the 4-ary system. The DNA codons in this table are listed for future reference.
5. A Probability density function for divisibility of integers. We have previously shown that if each integer from the TOH:2 series , 12131214 , is reduced by 1 unit, the indices of Table 2 : 01020103 result. If the zeros are removed from this series, the TOH:2 series is replicated. This process can be repeated ad infinitum and also applied to the generalized TOH:n series to reveal the self-similarity of the TOH:n series. The following theorem is the result of this self-similarity process. Theorem: The probability p that a randomly chosen integer
is divisible by nd but no higher power of n is
given by,
p(nd) = (1-x)xd (3) where x = 1/n. Proof:Since
every n-th integer is divisible by n, the probability x
that
an integer is divisible by n is x
= 1/n , and the
probability that an integer is not divisible by n
is 1-x.
Therefore, the probability that an integer has index 0 (not divisible by
n)
in the TOH:n table corresponding to
Table 4 is
1-x while the probability that it has a non-zero index (divisible
by n) is x. By the self-similarity of the TOH:n series,
the probability that an integer has index 1 (divisible by n1
but no higher power of n) is (1-x)x, while the probability
that the index is 2 or higher (divisible by all powers of n greater
than 1) is x2. That the probability of an integer having
index
d is (1-x)xd follows by induction.
Corollary:
Proof: Since
The corollary follows from p(nd) = (1-x)xd . Example 1: The probability that
an integer is divisible by 32 but no higher power of 3 is (1-1/3)(1/3)2
= 2/27. Therefore the number of integers smaller than 137 and divisible
by 32 but no higher power of 3 is approximately: (2/27)(137)
= 10.148 @ 10 as derived above. The numbers
are: 9,18,36,45,63,72,90,99,117,126. This result is approximate since the
probability distribution applies asympotically as the integer approaches
infinity. The probability distribution function given by Equation
4 is:
where the numbers above the terms in
this equation refer to the probability distribution of 1,3,32,33,
e.g.,
the total number of integers less than 137 divisible by any power of 3
is the sum of terms 1,2,3, and 4 of this probability distribution multiplied
by 137 or
Example 2: The relative frequency
of clockwise (CW) movements of the TOH:2 disks is gotten by adding the
even terms of Equation 4, to get 1/(x+1), while
the relative frequencies of the counterclockwise (CCW) terms are gotten
from the odd terms of Equation 4, or x/(1+x)
=1-1/(1+x) . For example, for TOH:2 x = 1/2, and two-thirds
of the moves are CW while one-third are CCW, a ratio of CW to CCW movements
of 2:1. Note that 1/(1+x) and x/(1+x) are the pair
of terms of the Farey series resulting from the fraction x = 1/n.
6. Relationship between 2-ary Gray Code and the
We have shown that the Towers of Hanoi puzzle is intimately connected
with the divisibility of integers. However, this game arises mysteriously
in other places in the mathematical terrain, most notably, in the symbolic
dynamics of the logistic equation of dynamical systems theory.
The logistic equation of dynamical systems theory [3]
is given by,
Given a sufficiently small value of a and beginning with x0 on the interval [0,1], the successive iterates (considered to be time intervals) of Equation 5 constitute a trajectory on [0,1]. It is well known that as values of a are increased to the critical value of 3.5699 , the trajectories approach periodic orbits of periods 2n for n = 1,2,3, For values of a exceeding the critical value, the system enters the realm of chaos in which small changes in the initial conditions result in wildly different trajectories given a sufficient number of iterates (time). If we label values of xn by 0 if they lie either at the maximum point or to the left of the maximum point of the logistic function y = ax(1-x) , and 1 if they lie to the right of the maximum, the resulting string of 0s and 1s is known as the symbolic dynamics of the logistic equation. The symbolic dynamics of the logistic equation can be generated from the binary sequence of integers in two steps: a) Add the digits of the binary numbers mod 2 to get the so-called Morse-Thue sequence [3] , e.g, 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, ® 0 1 1 0 1 0 0 1 1 0 0 b) The symbolic dynamics is gotten by transforming the Morse-Thue sequence to Gray code by Algorithm 3. This is equivalent to adding adjacent binary digits mod 2 to get what we refer to as the Complementary Morse-Thue sequence (CMT). Notice that the symbolic dynamics of the CMT sequence
is equivalent to the parity of the Towers of Hanoi sequence 121312141213121
where even digits are assigned 0 and odd digits 1 (i.e., CW = 1 and CCW
= 0). Therefore, the 1s and 0s of CMT are governed by the probability
density function of Equation 3, i.e., the ratio of 1s
to 0s is 2:1.
7. The Relationship between 4-ary Gray Code and DNA The 64 three letter code words, known as codons, that make up DNA can be encoded by a base four number system in a natural way. However, when the encoding numbers are represented by 4-ary Gray code this system has additional biological meaning. It is well known that DNA is composed of 64 codons.
Each codon is a three letter "word" made up of one of four bases C (Cytosine),
A (Adenine), G (Guanine), U/T (Uracil/Thymine). There is a natural way
to relate the DNA codons to Gray code. Use the following assignments:
For example CUG ® 011 and GAC ®
100. GAC is called the anti-codon of CUG since
1 of the codon is replaced by 0 and 0 by 1 of the codon to get the anti-codon. Notice that the upper and lower bit strings of both the codon and anti-codon differ in a single bit, e.g., they have a Hamming distance of 1. Subtracting the Hamming distance from 9 yields the number of hydrogen bonds per codon/anti-codon pair [7]. For example, both CUG and GAC have 9 1 = 8 hydrogen bonds.
In Table 6 the codons are arranged in an 8×8 square pattern along with their number of hydrogen bonds. In this square both the row and column numbers are labeled 0 to 7 in the standard Gray code, e.g., 000, 001, 011, 010, 110, 111, 101, 100, and each element of the table is listed by a 6-bit representation. This is equivalent to a Karnaugh map for a Boolean system with six variables. The Karnaugh map is a commonly used tool to simplify compound statements in Boolean (2-valued) logic [8]. In this table, as in all Karnaugh maps, adjacent elements to the left, right, up, down, or wrap-around of any element differs from that element in a single bit. Also to find the location of an anti-codon given the position (row and column) of a codon, or vice versa, use the following algorithm: row (column) 0 matches row (column) 5, 1 matches 4, 2 matches 7, 3 matches 6. For example, GGU is located in row R4 and column C5 which becomes R1 and C0 for the anti-codon CCA and each have 8 hydrogen bonds. It has been found that the amino acids are formed from contiguous groups of codons, e.g., proline: CCC, CCU, CCA, CCG; glutamine: CAA, CAG; leucine: CUU, CUC, CUG, CUA, UUA, UUG; etc. [7]. Apparently Gray code arises in genetics as a means of minimizing the "cliffs" or mismatches between the digits encoding adjacent bases and therefore the degree of mutation or differences between nearby chromosome segments. The requirement in an encoding scheme is that changing one bit in the segment of the chromosome should cause that segment to map to an element which is adjacent to the premutated element. There is a natural relationship between 4-ary Gray code and the DNA codons which can be understood by making the following correspondences: 0® C, 1®
A, 2® G, 3®
U/T in Table 5 and C ®
0, A® 0, G ®
1, U/T ® 1 in Table
6.
This enables Table 6
to be rewritten as Table 7 using the 4-ary Gray code
in Table 5. The corresponding decimal values are listed
in Table 8. For example, the bit string in Row 3, Column
7 of Table 6 is
which corresponds to UAG or Gray code
312 according to Table 7 or decimal 50 according to
Table
8. Notice that Table 7 inherits the property that
each codon differs from an adjacent codon: up, down, right, left, wrap-around,
in a single bit. Table 7 reveals the 4-ary number system
as the natural system with which to characterize the DNA codons. The integers
from 0 to 63 are divided into four quadrants. Each quadrant is subdivided
into four compartments of four codons where each digit of the codon representation
follows the pattern:
Table 7. 4-ary Gray Code Matrix
The circle of Figure 3 is another representation of the DNA codons as a 4-ary system. The circle is divided into four compartments labeled C,A,G,U. Each compartment is subdivided into four compartments with each compartment containing four codons. The codons, their number of hydrogen bonds, and decimal values according to Table 5 are arranged in the circle with each codon connected by a line to its anticodon. The following rules match codon with anti-codon: a) For decimal numbers 0 through 31, perform the operation of taking the mod 4 value. If the result is 0 or 1 then add 34. If the result is 2 or 3 then add 30. b) For decimal numbers 32 through 63, perform the operation of mod 4. If the result is 0 or 1 then subtract 30. If the result is 2 or 3 then subtract 34. For example, according to Table 5, GGU corresponds to decimal 35 where 35 mod 4 = 3. Therefore, according to rule b, subtract 34 to get decimal 1 which corresponds to CCA the anticodon of GGU. 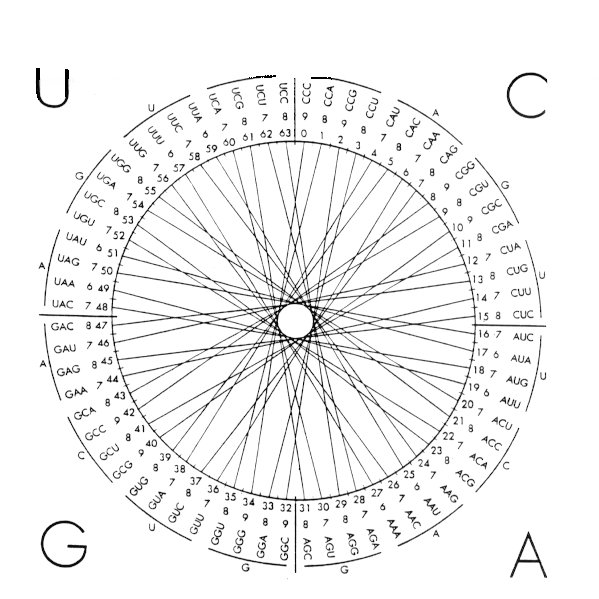
Figure 3. 4-ary circular representation of the
64 DNA codons
Conclusion Galileo stated that, "Natures great book is written
in mathematical symbols." We have shown that we can uncover the secrets
of number by holding it up to the light in the proper way. Information
about naturally occurring resonances, the nature of dynamical systems,
and the structure of DNA are already built into the number system through
a natural hierarchy of rational numbers. The Farey sequence and continued
fractions were introduced as tools to facilitate an understanding of this
hierarchy. We have also shown that the structure of the integers in terms
of their divisiblilty is isomorphic to the Towers of Hanoi puzzle and its
generalizations. Gray code and its generalizations was introduced as an
aid to understand this puzzle and also as the natural framework for systematizing
the 64 codons of DNA.
Given the indices of a compound fraction expansion, p/q = [a1,a2,a3, ,an], the approximating rational numbers, called approximants, obtained by truncating the compound fraction at successive levels can be computed by the following procedure: 1. Invert the first index so that the
first approximant is p1/q1 = 1/a1.
pn+1/qn+1 = (an+1pn + pn-1)/(an+1qn + qn-1). The pn/qn approximant is the best approximation to p/q by a rational number with denominator no larger than qn. For example, [3,1,2] is found as follows: 3 1 2
Therefore, 1/4 is the best approximation to 3/11 with denominator no
larger than 4 while 1/3 is the best approximation to 3/11 with denominator
no larger than 3.
The following algorithm determines the irrrational number corresponding to the periodic continued fraction [a1,a2, an]¥ 1. Form a matrix from the last two approximants a/b, c/d derived as in Appendix A, e.g.,
2. The irrational number is c/Q where Q = l1 - a with l1 the larger of the two positive eigenvalues l1 and l2 of the matrix A. 3. By the nature of continued fraction expansions, the determinant of the matrix always equals 1 when there are an odd number of indices, and +1 when there are an even number of indices. Therefore, it is easy to show that l1 satisfies one of the following characteristic equations: l1 - 1/l1 = Trace(A) = a+d if odd number of indices (B1) l1 + 1/l1 = Trace(A) = a+d if even number of indices and that Trace A = l1 + l2 where, l2 = -1/l1
if odd number of indices
Since the solution to l -
1/l = 1 is the golden mean or t
= (1+ Ö 5)/2, I shall refer to the solutions
to Equations B1 as generalized silver means of type 1 and type 2, i.e.,
l1
= SM1(n) for odd indices and l1
= SM2(n) for even indices. Therefore, golden mean
t
= SM1(1).The generalized silver mean has property that
the sum of it and plus or minus its inverse is an integer. Note that the
same holds for any power of the generalized silver mean, i.e., lm±
(1/l )m = Integer. This follows
from the fact that lm and
(1/l )m or (1/l
)m are eigenvalues of Am, the matrix
corresponding to m repetitions of the indices of the corresponding
rational number.
Example 1: From the example in Appendix A, [3,1,2]¥ = 3/(l1 - 1) where l1 satisfies, l - 1/l = 12 and 12 is the trace of the matrix
Solving for l1 gives l1 = SM1(12) = 6 + Ö 37. Therefore, [3,1,2]¥ = 3/(5 +Ö 37) = 0.2707 (compared with 3/11 = 0.2727). Example 2: From Appendix A, the approximants corresponding to indices [1,2]¥ are, 1 2
And, [1,2]¥ = 2/(l1 -1) where l1 + 1/l1 = 4 (an even number of indices) where 4 is the trace of
The approximants corresponding to [1,2,1,2] are 1 2
1 2
Therefore the matrix corresponding to [1,2,1,2]¥
is
where A is the matrix corresponding to [1,2]¥
and, Trace A2 = (l1)2
+ (1/l1)2 = 14 where
l1 = 2 + Ö3.
You may check to see that [1,2]¥
= [1,2,1,2]¥.
Given a rational number P/Q where P<Q, the Euclidean Algorithm can be used to determine the indices of the continued fraction representation. The Euclidean Algorithm is based on the division algorithm in which an integer a divided by a positive integer d can be expressed in terms of quotient q and remainder r as: a = qd + r where 0£r<d Apply the division algorithm division algorithm recursively beginning with q/p as follows : Q = q1P + r1
where r1> r2 > >rk> >1> 0 That next to the last remainder equals 1 reflects the fact that P and Q are in lowest terms. The continued fraction representation of P/Q is then [q1,q2, ,qn]. For example, consider 7/10:
The following algorithm may be used to determine the rational number corresponding to a Gray code representation of a given integer: a) Add a zero to the end of the Gray code number. b) In the Gray code representation starting from left to right, replace the following strings by the corresponding integers: 1 º 1, 10 º 2, 100 º 3, 1000 º 4, etc. c) The resulting sequence of integers are the indices of the continued fraction. For example, in Table 1 the integer 14 is represented
in Gray code by 1001. Adding a 0 gives 10010. Replacing 100 by 3 and 10
by 2 yields the continued fraction [3,2] = 2/7.
Bibliography
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||